Commercializing Alternative Architectures, Part 1

Cartesia's State Space Models

This post is the first of a two-part series on startups commercializing non-transformer models. I’ve endeavored, sometimes via footnotes, to make this post clear for non-technical folks as well.

I recently spent some time digging into state space models (SSMs) and Cartesia,¹ the startup commercializing them that raised a $64M Series A led by Kleiner Perkins this week. In this post, I’ll cover how SSM neural nets stack up against transformers, the currently dominant architecture, and why I’m bullish on the startup: Although the company is currently focused on text-to-speech (TTS), SSMs could be more broadly game-changing for audio, video, and robotics. With Deepseek’s cheap training claim still on everyone’s minds, it also doesn’t hurt that there’s theoretical and empirical evidence that SSMs can be trained much more cheaply than transformers can. I’ll also discuss some of the risks I see for the company.

I. A Quick Theory Primer

The S4 paper, published by the founders in 2021, describes the basic concept of SSMs, how to approximate them to arrive at two forms that are used respectively for training and inference, and how to use SSM layers to build a model. To summarize here, their SSM is defined by the following two equations:

\( \begin{flalign} & x'(t) = Ax(t) + Bu(t) \\ &y(t) = Cx(t) \end{flalign} \)

where x(t) is a vector, u(t) is a scalar input, and y(t) is a scalar output.² The parameters to be learned are the matrices A and C and the vector B.

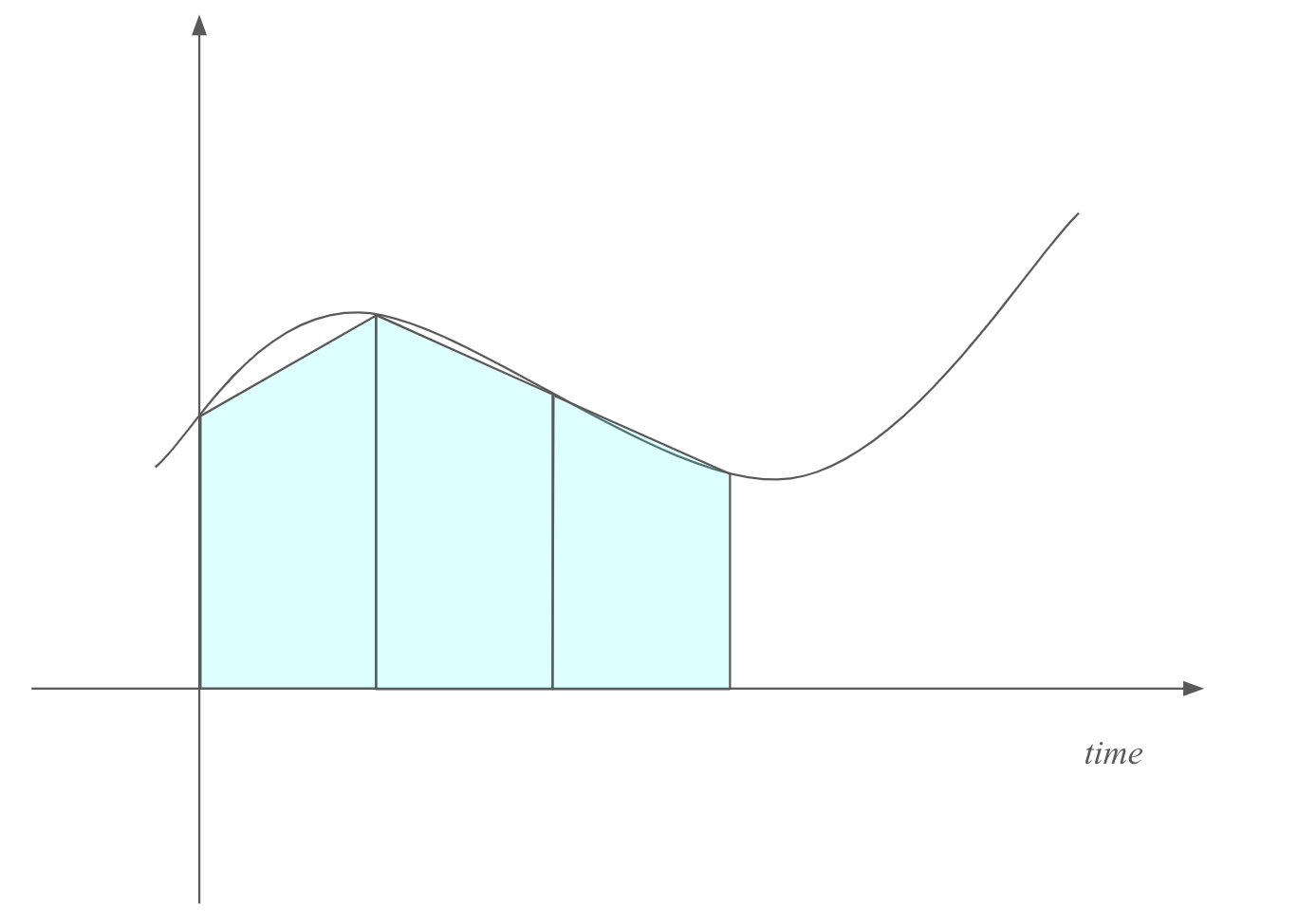
To arrive at the first, recurrent³ form of these equations, they integrate both sides of the first equation by t and approximate the right side’s integral with the trapezoidal method (see Fig. 1 for a quick visual explanation of the approximation), which results in

\(\begin{flalign} & x_k = Fx_{k-1} + Gu_k \\ &y_k = Cx_k \end{flalign}\)

where F and G can be written in terms of A, B, and the time delta between the inputs. k here represents the time step, as in u₁ is the input at time step 1, u₂ is the input at the next time step, etc. Note that the time delta is a constant, i.e. this discretization assumes that the time steps are evenly spaced. This recurrent form is used for inference.

To arrive at the second, convolutional⁴ view, they use the above recurrence to write y_k in terms of u₀, u₁, u₂…, and u_k and not in terms of any x. The convolutional form is used for training.

The above SSM takes in 1-dimensional inputs and produces 1-dimensional outputs. So in order to process N-dimensional inputs, they combine N SSMs, one for each dimension, in an SSM layer. The overall architecture (eliding a few details⁵) is then a stack of these SSM layers. (Note that many articles use the term “SSM” to refer to the definition provided above and to a whole architecture that uses SSMs.)

The founders and other research groups have published variations and improvements on the above, but S4 should still provide a good mental model for how SSMs can be applied to ML.

Figure 1. Using the trapezoid approximation to approximate the integral for three time steps.

II. Long Contexts on the Cheap

One of the company’s core pitches is that they can provide very long context windows at lower cost than transformer-based platforms can, and that these long windows will give them an edge in processing long-sequence data like genomics data and audio and video streams⁶.

This pitch is rooted in the training time complexity (i.e., number of operations needed for training) of SSMs and transformers: The complexity of the convolutional view of SSMs increases approximately⁷ linearly with sequence length L. For transformers, complexity increases quadratically⁸. These complexities mean it takes about twice as much work, using an SSM architecture, to double the length of the context window and four times as much work with a transformer architecture. (Technically the previous sentence, from a mathematical perspective, is not guaranteed to be true for small L, but the founders have shown experimentally that SSMs can be trained more quickly for small L; see Table 3 from the S4 paper.)

There’s also evidence that SSMs may be better at tracking relationships across long contexts, with SSMs outperforming transformers on problems like Path-X⁹. So Cartesia could have a significant advantage on processing large amounts of data and having an understanding of the data that spans its entire length.

III. Local Inference for Safety-Critical Applications

Another major pitch of the company is being able to provide low-latency, network-fault-tolerant inference, which I’d expect to have a market in safety-critical robotics. (You wouldn’t want machinery handling fragile or dangerous materials to fail to react to changing conditions because of slowness or a network blip.)

Their pitch is that they’ll be able to provide those two properties by deploying models directly on your local hardware, so that the network’s attendant latency and intermittent failures are no longer on the inference path. They expect to achieve local deployment on hardware that is lower-end than datacenter inference servers because SSMs require constant memory for inference. This property should be clear from the recurrent form of the SSM: F, G, C, and x are of constant size, so the amount of memory you need is the same regardless of whether you’re trying to calculate the first output or the millionth. In contrast, transformers require a growing amount of memory with each token, even if they use FlashAttention-2, the most memory-efficient published method. (Furthermore, many transformer implementations use a KV cache, which re-uses work done for previous tokens. The cache grows with each additional token processed.)

IV. The Flipside

The use cases for long contexts and local deployment are compelling, but what are sources of uncertainty for the technology and the company?

With respect to the language domain, further research is likely necessary to make SSMs competitive with transformers. SSMs have been shown to do well on some language benchmarks (see Table 3 from the Mamba paper), achieving results comparable to transformers with twice the number of parameters. However, a Harvard research group also published a paper showing that SSMs don’t do as well at copying information: Given a phone book and a name, SSMs have markedly worse performance than transformers on looking up the exact phone number (see their Figure 1c). They suggest exploring hybrid attention¹⁰ and SSM architectures for language modeling, and I wouldn’t be surprised if current market leaders like Open AI have already gotten a head start on conducting this research at scale.

Cartesia also has competitors in the voice space: For example, Open AI has a TTS product. However, with no support for emotions, different sample/bitrates, or sequences longer than 4096 characters, Open AI’s offering seems relatively basic. ElevenLabs, which recently raised a 180M series C and acquired AI agents startup Decagon as a customer, has a more feature-ful offering and is a more serious competitor.

V. Conclusion

Cartesia has an incredible founding team of Stanford PhDs from lab with a track of record of producing unicorns like Snorkel.ai and SambaNova. The founders are responsible for foundational work on SSMs for ML, and the tech has significant potential for audio, video, genomics, and robotics. I think Cartesia’s investors have made a smart bet, and I’m excited to see what the team develops with their new funding.

Thanks for reading. Comments welcome. Stay tuned for part 2 on Liquid AI.

Updates: March 14: Updates for clarity. March 15: Updated to reflect that I think more than one architecture will be used in robotics. March 17: Updates for tone. March 19: Small update to section I to clarify which form of the SSM is used for training, and which for inference.

1. Full disclosure, I had the good fortune of working in Chris Re’s lab as a masters student so I have a lot of respect for Chris and his PhD students.

2. Substack, can we please have inline math typesetting?

3. So named because in this view, each x is written in terms of the previous x.

4. In machine learning, a convolution typically refers to element-wise multiplication of a filter and an input, followed by a sum, at every position that the filter is applied. For example, if you have a filter [1,2] and you apply it to an input [1,2,3,4], shifting the filter by two spaces at a time (so that you apply it to the first two then the last two elements of the input) your output would be [5, 11]. Here we end up writing y_k as a filter applied to [u₀, u₁, u₂…, u_k].

5. The architecture also incorporates linear layers and non-linearities, which are both fairly standard components in ML.

6. See the abstract in the Mamba paper.

7. Eliding a logarithmic factor. Since the log function grows extremely slowly, in computer science we sometimes say that it is basically constant:)

8. See Table 1 of the S4 paper.

9. The problem is to ascertain whether two points in an image are connected by a dotted line, and outperforming refers to being able to make this determination on a larger image. Essentially, SSMs can track across a longer sequence of pixels whether the two points are connected or not. See section 4.2 of the S4 paper for the SSM results on this problem.

10. A core part of transformers that models relationships across a sequence. See “Attention is All You Need.”